Capacidad: Utiliza el vocabulario y la notación matemáticos, según contextos que lo requieran: números binarios.
Sistema binario de números
Un número binario solo tiene ceros y unos. Dos valores diferentes.
Como solo puedes tener ceros y unos, en binario se cuenta así:
Decimal: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Binario: 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111
El binario es tan fácil como 1, 10, 11.
Aquí tienes más equivalencias
Decimal: 20 25 30 40 50 100 200 500
Binario: 10100 11001 11110 101000 110010 1100100 11001000 111110100
La palabra binario viene de «bi» que significa dos.
Cuando leas un número binario, pronuncia cada dígito (por ejemplo, el número binario « 101» se lee «uno cero uno». De esta manera la gente no los confunde con números decimales.
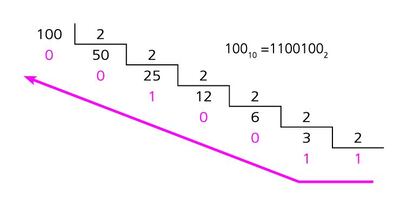
Para pasar del decimal al binario, se hacen divisiones sucesivas de número entre dos, como en el ejemplo:
Como puedes ver, la flecha nos indica el sentido en que se debe escribir el número binario que corresponde, se comienza con el último cociente hasta el primer residuo.
Para diferenciar un número binario de un número decimal, se coloca el subíndice 2 al final del número binario, como está en el ejemplo.
Pero si lo que se desea es pasar de la numeración binaria al la decimal, entonces se procede de la siguiente manera:
a) Se enumera dada dígito del binario, en la parte superior como en el ejemplo, comenzando desde el cero, para indicar los exponentes que tendrán las potencias de dos (2).
b) Se escribe la suma de las potencias de dos, multiplicadas cada una por el dígito que corresponda del binario.
c. Se suman estos productos para obtener el decimal que corresponde.
1101012 = 1.25 + 1.24 + 0.23+ 1. 22 + 0.21+1. 20 = 32+ 16+0+4+0+1= 53
Fuente
Recuperado de: http://www.aula365.com/codigo-de-barras-y-sistema-binario