Cargando...
Capacidad: Utiliza el vocabulario y la notación matemáticos, según contextos que lo requieran. Números binarios.
Esta codificación se basa en el sistema de numeración binario y responde a regulaciones que se aplican a nivel mundial.
Este sistema de codificación le otorga a cada producto un número propio que lo identifica en todo el mundo. La representación de este número a través de barras negras y espacios en blanco, permite que pueda ser leído por los sistemas ópticos.
Los productos de consumo masivo utilizan la codificación EAN-13, que consiste justamente en 13 dígitos y sus correspondientes barras y espacios, similar a la imagen anterior. Los tres primeros, de izquierda a derecha, corresponden al país de origen. A la Argentina le corresponde 477. En el ejemplo, 380 significa Bulgaria. Los nueve dígitos que siguen identifican al fabricante y al producto. El último es un dígito de verificación.
El mundo digital está basado en el sistema de numeración binario y los códigos de barra son una muestra de la infinidad de aplicaciones que pueden desarrollarse utilizando solamente ceros y unos. Veamos cómo se interpretan las barras.
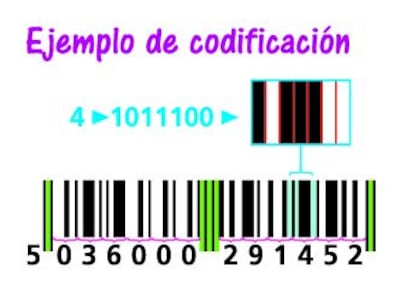
Aquí podemos ver un ejemplo de codificación. Cada dígito del código está representado por dos barras y dos espacios que se distribuyen en siete módulos binarios. El grosor de las barras y los espacios determina la interpretación que realizará el lector láser. En este caso, el dígito 4 está representado, de izquierda a derecha, por una columna de un módulo, un espacio de un módulo, una columna de tres módulos, y un espacio de dos módulos. De acuerdo a esto, la decodificación binaria del 4 en este caso es 1011100, que equivale a 1.132 en base 10.
Fuente: Recuperado de: http://www.aula365.com/codigo-de-barras-y-sistema-binario/