Cargando...
Es evidente que, en problemas geométricos, la construcción de figuras es de suma importancia para la comprensión, pero es de destacar que, también en problemas aritméticos y algebraicos, son de gran ayuda para la solución de los mismos.
Ejemplo 1
De un depósito lleno de agua, se saca la tercera parte del contenido. Después se saca la mitad de lo que quedó. Finalmente quedaron en el depósito 1200 litros de agua. ¿Cuál es la capacidad total del depósito?
Es importante aclarar que el problema se puede resolver utilizando fracciones, pero ahora nuestra intención es practicar la técnica de “hacer un dibujo” para resolver un problema.
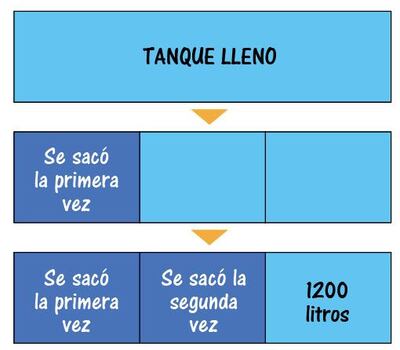
Trazamos un rectángulo de dimensiones arbitrarias (la figura no es lo fundamental), lo dividimos en tres partes iguales y pintamos una de ellas, que corresponde a la primera extracción de agua.
Luego pintamos otra de las partes, que corresponde a la mitad de lo que quedó.
Al final nos queda el último rectángulo de la secuencia de abajo.
Al observar las figuras y teniendo en cuenta los datos que aparecen en las mismas notamos que 1200 litros corresponde a la tercera parte de la capacidad total del tanque. Entonces 1200 x 3 = 3600 litros es la capacidad total del tanque.
Ejemplo 2
En una casa hay 8 mesas en total, algunas tienen 4 patas y otras tienen 3 patas. En total hay 27 patas. ¿Cuántas mesas de cada tipo hay?
Dibujamos 8 mesas y a cada una le dibujamos 3 patas.
Observamos así, que se tienen solamente 24 patas y faltan 3.
Agregamos una pata a algunas mesas hasta completar un total de 27 patas.
Observamos el dibujo y notamos que hay tres mesas con 4 patas y 5 mesas con 3 patas.
Ejemplo 3
La tercera parte de los árboles de la quinta de mi tío Raúl son naranjos, dos quintos son pomelos y el resto, son 12 plantas de mandarina. ¿Cuántas plantas tiene en total mi tío Raúl en su quinta?
Representamos todos los árboles de la quinta mediante un rectángulo y dividimos la quinta (rectángulo) en tres partes en forma vertical y en cinco partes en forma horizontal (por las condiciones del problema).
Pintamos 1/3 del rectángulo, que representa los naranjos.
Ahora pintamos 2/5, que representa los pomelos.
Observamos la cantidad de casillas ocupadas por cada tipo de planta y pintamos otro rectángulo de la siguiente forma.
La parte no pintada representa a las 12 plantas de mandarina.
Como cada casilla representa la misma cantidad y tenemos 4 casillas no pintadas, entonces 12: 4 = 3 es la cantidad de plantas de mandarina que representa cada casilla no pintada.
En total hay 15 casillas, que representan el total de plantas de la quinta y por lo tanto en la quinta hay en total 15 x 3 = 45 plantas.