Proporcionalidad inversa

En símbolos, A y B son inversamente proporcionales si y solamente si A. B = k.

Ejemplo 1

Lea más: Proporcionalidad directa

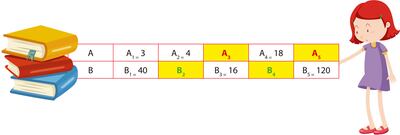
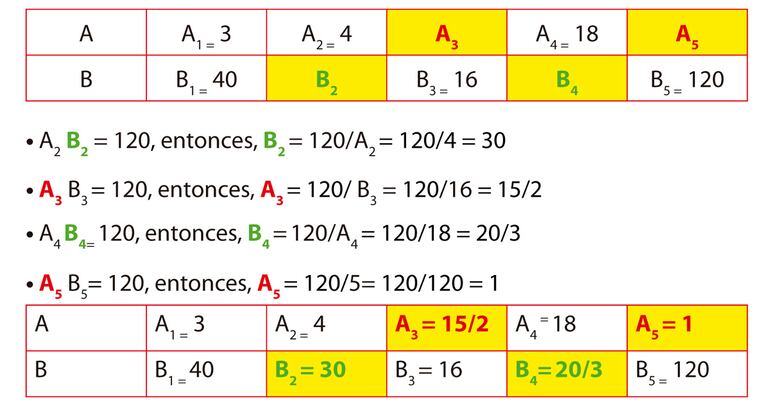
Completa la siguiente tabla sabiendo que la proporcionalidad entre las magnitudes es inversa.

¿Cuánto corresponde a 1?

Todos los beneficios, en un solo lugar Descubrí donde te conviene comprar hoy

Como ya sabemos que A y B son inversamente proporcionales, entonces A B = k y al ser la primera pareja de valores de la tabla los números 3 y 40, escribimos 3. 40 = k, entonces el valor de k = 120 y de ese modo podremos obtener los demás valores de la tabla a partir de «k».

Para facilitar la explicación, usaremos subíndices para diferenciar los valores que queremos encontrar, sin embargo, una vez comprendido el procedimiento, esto ya no es necesario.

Ejemplo 2

Si 9 obreros hacen una obra en 120 días, ¿en cuántos días lo podrán hacer 12 obreros?

Ejemplo 3

¿Cuántas cajas de 16 kg de frutillas se necesitan para tener el equivalente a 56 cajas de 24 kg cada una?

Actividad

Indica si la tabla es de proporcionalidad directa o inversa.

________¿Por qué? ______________________________

________¿Por qué? ______________________________