Proporcionalidad directa

Cuando los datos de una situación problemática pueden cambiar, le damos el nombre de variables. A aquellos datos que no dependen de otros les llamamos variables independientes y a los que dependen de otros les llamamos variables dependientes. Por ejemplo, el volumen de un cubo depende directamente de la longitud de su arista; en una transacción de negocio, el precio de un lote de artículos depende de la cantidad de artículos que tenga el lote; la distancia que recorre una móvil depende de la cantidad de tiempo que emplea en hacerlo.

Cuando una variable depende de otra, decimos que es función de ella, y en los ejemplos que hemos citado más arriba, podemos decir que el volumen del cubo es función de la longitud de la arista, el precio del lote de artículos es función de la cantidad, la distancia recorrida es función del tiempo empleado.

Lea más: Ecuaciones cuadráticas. Ejercicios de aplicación

Las leyes de dependencia de dos variables pueden ser complicadas en algunas ocasiones. Sin embargo, en muchas aplicaciones matemáticas existe una ley de dependencia funcional muy simple, llamada proporcionalidad, la cual puede ser directa o inversa.

Proporcionalidad directa

Dos variables A y B son directamente proporcionales si el cociente de A por B, llamado razón de A a B se mantiene constante cualesquiera sean los valores de A y B elegidos.

En otras palabras, A y B son directamente proporcionales si y solamente si (constante), es decir, si y solamente A = k B.

Cuando dos magnitudes son directamente proporcionales, decimos simplemente que son proporcionales.

Si representamos por «p» la cantidad de personas que suben a un bus y por «r» la recaudación del bus, como la recaudación es directamente proporcional a la cantidad de personas que viajan, podemos escribir r = k p

Ejemplo 1

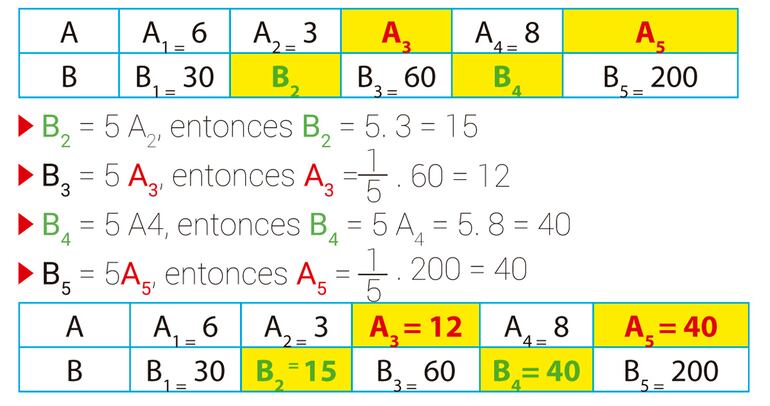
Si sabemos que las magnitudes A y B son directamente proporcionales, podemos completar fácilmente la siguiente tabla.

Como ya sabemos que A y B son directamente proporcionales, entonces B = k A y al ser la primera pareja de valores de la tabla los números 6 y 30, escribimos 30 = k 6, entonces el valor de k = 5 y de ese modo podremos obtener los demás valores de la tabla a partir de k.

Para facilitar la explicación, usaremos subíndices para diferenciar los valores que queremos encontrar, sin embargo, una vez comprendido el procedimiento, esto ya no es necesario.

Ejemplo 2

Un poste de 6 metros de altura proyecta una sombre de 2 m de longitud. Determina la altura de un edificio que a la misma hora proyecta una sombra de 30 metros.