Cargando...
Operaciones y sus propiedades
Adición
Para determinar la suma de dos enteros, es importante tener en cuenta sus signos, según lo siguiente:
- Si ambos son positivos o uno de los dos es cero, simplemente se deben sumar sus valores absolutos y se conserva el signo positivo.
Ejemplo: 3 + 5 = 8.
- Si ambos signos son negativos o uno de los dos es cero, simplemente se deben sumar sus valores absolutos y se conserva el signo negativo.
Ejemplo: -5 + -3 = -8
- Si tienen signos diferentes, se debe restar el valor absoluto del menor al del mayor y se conserva en el resultado el signo del mayor.
Ejemplo: -3 + 5 = 2 y 3 + (-5) = -2
En resumen, si Z+ y Z- y representan los enteros positivos y negativos respectivamente, entonces
Lea más: Los números enteros
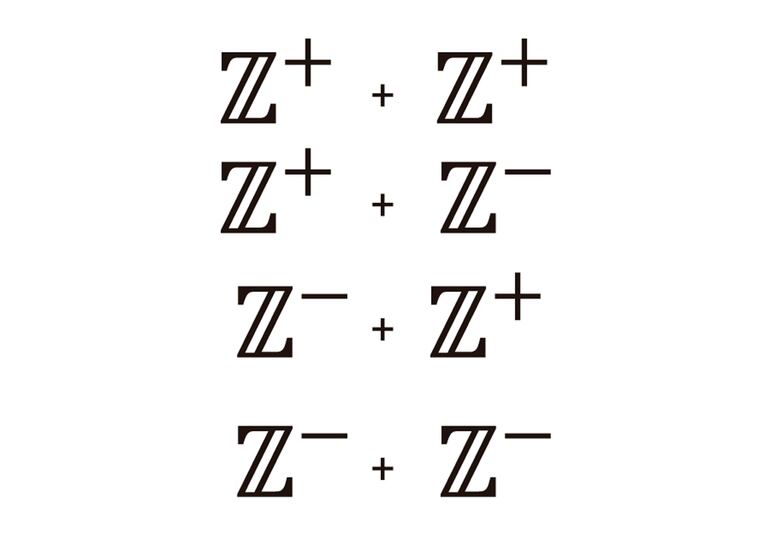
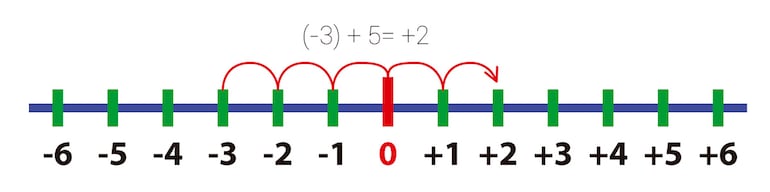
Si para comprender mejor usamos la recta numérica, debemos tomar como referencia el cero, recordando que las cifras negativas se posicionan a la izquierda del cero y las positivas a su derecha y que al adicionar dos enteros, estos deben moverse a partir del cero tantos lugares como indique su valor absoluto. Observemos el siguiente ejemplo.
Propiedades de la adición de números enteros
1) Clausura: la suma de dos números enteros es siempre otro número entero.
2) Conmutativa: si a y b son números enteros, entonces a + b = b + a.
3) Asociativa: si a, b y c son números enteros, entonces (a + b) + c = a + (b + c).
4) Existencia del elemento neutro: para todo número entero «a» existe un único entero «0» tal que a + 0 =0 + a = a (si a cualquier entero le sumamos el «cero», resulta el mismo número).
5) Existencia del elemento inverso (opuesto): para todo entero «a» existe un único entero «-a» tal que a + (-a) = (-a) + a = 0 (la suma de un entero con su opuesto es siempre igual a su elemento neutro, el cero).
Actividades
1 Resuelve las siguientes adiciones usando la recta numérica
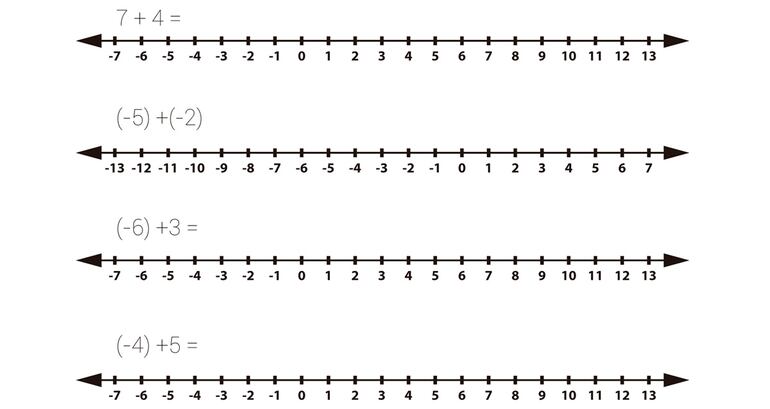
2 Resuelve las siguientes adiciones usando el concepto del valor absoluto.
a) -5 + 12= b) - 18 + 7 = c) (-8) + (-8) = d) 15 + (-7) = e) 5 + 5 =
Respuestas
1) 11; -7; -3;1
2) a) 7; b) -11; c) -16 d) 8; e) 10