Cargando...
Es importante tener en cuenta que una ecuación lineal con dos incógnitas x e y se puede representar en forma gráfica en un plano cartesiano.
Por ejemplo, la ecuación 5x - y - 2 = 0
Para que la igualdad sea cierta, se deben encontrar los valores de x e y tales que al reemplazarlos en la ecuación satisfagan la misma.
Para encontrar los valores de x e y se despeja una de las variables de la ecuación en función de la otra. Si, por ejemplo, despejamos la variable y en función de x, nos queda
Y = 5x -2
Al elegir diferentes valores para la variable independiente x, obtendremos valores para la variable dependiente y.
Así:
- Al considerar x = 1, se obtiene y = 5 . (1) - 2= 3.
- Al considerar x = 2, se obtiene y = 5 . (2) - 2= 8.
- Al considerar x = -1, se obtiene y = 5 . (-1) - 2= -7.
- Al considerar x = 0, se obtiene y = 5 . 0 - 2= -2.
Los puntos que hemos podido determinar son
M (1, 3); N (2, 8); P (-1, -7) y Q (0, -2).
Marcamos los puntos en un plano cartesiano y los unimos mediante una línea recta.
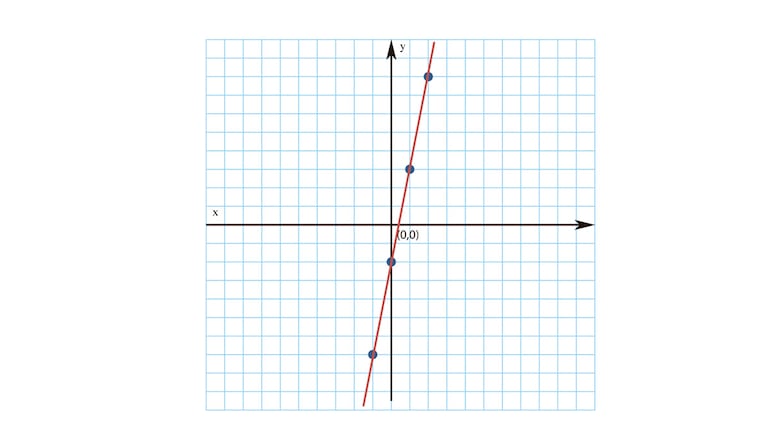
Hemos utilizado el ejemplo para explicar que una ecuación de primer grado con dos incógnitas se representa gráficamente mediante una recta.
Como al resolver un sistema de dos ecuaciones lineales con dos incógnitas nuestro objetivo es encontrar los valores de x e y que satisfacen ambas ecuaciones, podemos asociar este hecho con que dichos valores de x e y representan las coordenadas del punto común a ambas rectas representadas por las ecuaciones del sistema.
Para resolver un sistema de ecuaciones lineales en forma gráfica realizamos los pasos que describimos a continuación.
Lea más: Sistemas de dos ecuaciones lineales con dos incógnitas (1)
En el siguiente gráfico el punto donde se cortan ambas rectas, el punto (4,2) es la solución del sistema de ecuaciones.
Actividad
Resuelve gráficamente los siguientes sistemas de y ecuaciones lineales.
2x + y =7
x - y = 2
x + y =8
x - y = 2